Vous êtes ici
3.1.1. Le rôle mécanique de l’eau sur les berges
En fonction du régime hydrologique, de la structure de la berge et de la zone étudiée, l’eau peut avoir une action mécanique favorable ou défavorable sur la tenue de la berge. La berge est, on le rappelle, constituée d’un sol de granulométrie variable (grossière, fine ou mixte). L’eau joue ainsi un rôle complexe qui se décline à des échelles très différentes.
3.1.1.1. L’eau et les propriétés physiques du sol
La teneur en eau des sols fins
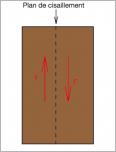 La teneur en eau du sol influence sensiblement ses propriétés physiques et plus spécialement sa résistance au cisaillement. Le cisaillement correspond à une sollicitation tangentielle à la surface de laquelle sont appliqués ces efforts. Au plan de cisaillement, nous observons un glissement des particules de matière (fig. 1).
La teneur en eau du sol influence sensiblement ses propriétés physiques et plus spécialement sa résistance au cisaillement. Le cisaillement correspond à une sollicitation tangentielle à la surface de laquelle sont appliqués ces efforts. Au plan de cisaillement, nous observons un glissement des particules de matière (fig. 1).
La stabilité d’une berge, notamment vis-à-vis du glissement, est étroitement liée à sa résistance au cisaillement.
La résistance au cisaillement d’un sol saturé en eau est plus faible que celle d’un sol non saturé. Dans ce dernier, des forces attractives d’absorption entre les grains augmentent la résistance au cisaillement apparente du sol.
Cette force est à l’origine d’une cohésion apparente améliorant la qualité mécanique du sol.
Les épisodes de crue, en saturant le sol en eau, diminuent sa cohésion, augmentent les pressions interstitielles et favorisent les risques de glissement.
Il y a ainsi lieu de bien distinguer la cohésion, qui est source de stabilité, de la pression interstitielle, qui génère les risques les plus forts de glissement à la décrue (chap. II.3.1.4).
Isolée de toute contrainte extérieure, la stabilité de la berge est assurée grâce à sa géométrie (pente), sa composition (granulométrie, texture) et sa teneur en eau. Autrement dit, une augmentation de la teneur en eau peut modifier, à elle seule, l’état de stabilité de la berge.
La teneur en eau du sol est influencée par :
• le niveau du cours d’eau et de la nappe d’accompagnement ;
• la nature des matériaux constitutifs de la berge et notamment leur perméabilité ;
• les conditions météorologiques ;
• l’évapotranspiration de la végétation rivulaire.
• le niveau du cours d’eau et de la nappe d’accompagnement ;
• la nature des matériaux constitutifs de la berge et notamment leur perméabilité ;
• les conditions météorologiques ;
• l’évapotranspiration de la végétation rivulaire.
Les cycles de gel et de dégel
Les cycles de gel et de dégel sont à l’origine d’une destructuration mécanique du sol, aggravée par la présence d’eau dont le volume augmente à l’état solide. Plus la fréquence de ces cycles est élevée, plus la dynamique d’érosion est importante. Ce type d’érosion augmente avec l’altitude. Il a été démontré que la présence de végétaux, et même d’un enherbement épars, réduit les fluctuations de température dans le sol en limitant les vitesses de vent et les échanges de chaleur entre le sol et l’atmosphère. Il a également été observé que le couvert végétal diminue la fréquence du cycle de gel et dégel sur les berges de rivière et diminue ainsi les mécanismes d’érosion (Bohn 1989, dans Abernethy et Rutherfurd 1998).
3.1.1.2. Les actions mécaniques directes engendrées par l’eau
La vitesse du courant
La vitesse du courant fait partie des grandeurs caractéristiques d’un cours d’eau. Sa détermination se fait classiquement à partir des lois telles que Manning-Strickler ou Keulegan.
La formule de Manning-Strickler est souvent employée pour calculer la vitesse de l’eau en régime permanent et uniforme.
Le coefficient de rugosité K doit être calé sur des mesures de ligne d’eau. Il peut également être calculé à partir de la granulométrie du lit. Cependant, les modèles proposés ne sont plus valables lorsque la pente et le diamètre des blocs sont élevés.
Le coefficient de rugosité K doit être calé sur des mesures de ligne d’eau. Il peut également être calculé à partir de la granulométrie du lit. Cependant, les modèles proposés ne sont plus valables lorsque la pente et le diamètre des blocs sont élevés.
U=K.R2/3 .I1/2
Où :
• U = la vitesse de l’eau (m.s–1) ;
• K = le coefficient de rugosité (ou de Strickler) ;
• R = le rayon hydraulique (m) – rapport de la surface mouillée sur le périmètre mouillé ;
• I = la pente du cours d’eau (–).
Ces dernières donnent des résultats corrects pour des profondeurs relatives supérieures à 7 environ. La profondeur relative est définie par le ratio R/D84, où :
• R = le rayon hydraulique ;
• la granulométrie D84 = l’ouverture théorique du tamis telle que 84 % des particules ont un diamètre inférieur.
• R = le rayon hydraulique ;
• la granulométrie D84 = l’ouverture théorique du tamis telle que 84 % des particules ont un diamètre inférieur.
Mais ce domaine correspond à l’échelle des « petites rugosités » selon la classification proposée par Bathurst et al. (1981). Pour les plus faibles tirants d’eau (échelles des rugosités moyennes et larges), qui concernent la plupart des cours d’eau de montagne en écoulement de crue, ces formules surestiment les vitesses.
Pour les grandes rugosités, la formule de Manning-Strickler a été revue par Ferguson (2007). Cette formulation, dite « VPE » (Variable Power Exponent), permet de déterminer la vitesse à partir de la hauteur d’eau :

Où :
• a1 = 6.5 et a2 = 2.5 ;
• U = la vitesse d’écoulement (m.s–1) ;
• g = la pesanteur (m.s–2) ;
• J = la pente d’énergie prise à égale à la pente du cours d’eau dans notre cas (–) ;
• R = le rayon hydraulique (m).
• a1 = 6.5 et a2 = 2.5 ;
• U = la vitesse d’écoulement (m.s–1) ;
• g = la pesanteur (m.s–2) ;
• J = la pente d’énergie prise à égale à la pente du cours d’eau dans notre cas (–) ;
• R = le rayon hydraulique (m).
Dans le même esprit, Rickenmann et Recking (2011) ont proposé un calcul permettant de déterminer la vitesse à partir du débit unitaire q (débit par unité de largeur en m2s–1) :

En utilisant deux nouvelles variables adimensionnelles :

Où :
• U = la vitesse d’écoulement (m.s–1) ;
• g = la pesanteur (m.s–2) ;
• J = la pente d’énergie prise à égale à la pente du cours d’eau dans notre cas (–) ;
• R = le rayon hydraulique (m) ;
• D84 = le diamètre correspondant à 84 % des matériaux de diamètre inférieur sur la courbe granulométrique (m).
• U = la vitesse d’écoulement (m.s–1) ;
• g = la pesanteur (m.s–2) ;
• J = la pente d’énergie prise à égale à la pente du cours d’eau dans notre cas (–) ;
• R = le rayon hydraulique (m) ;
• D84 = le diamètre correspondant à 84 % des matériaux de diamètre inférieur sur la courbe granulométrique (m).
L’action mécanique de l’eau
L’eau exerce un effort sur les parois du lit. La force dF exercée sur une unité de surface dS, peut être décomposée dans un plan normal à une paroi de la manière suivante :
• la force tractrice dFt, composante parallèle à la paroi (fond ou berge) et dirigée dans le sens de l’écoulement ;
• la force normale dFN , liée à la pression de l’eau par la relation dP = dFN .dS avec dP, pression élémentaire de l’eau sur dS. Cette composante est perpendiculaire à la paroi.
• la force tractrice dFt, composante parallèle à la paroi (fond ou berge) et dirigée dans le sens de l’écoulement ;
• la force normale dFN , liée à la pression de l’eau par la relation dP = dFN .dS avec dP, pression élémentaire de l’eau sur dS. Cette composante est perpendiculaire à la paroi.
La contrainte tractrice (ou de cisaillement ou d’arrachement)
La force de frottement de l’eau, ou force tractrice, génère une contrainte sur le lit du cours d’eau. Cette contrainte tractrice τ représente la contrainte tangentielle de la colonne d’eau exercée sur la paroi du chenal :

Où :
• τ = la contrainte tractrice (N.m–2) ;
• dFt = la force de frottement élémentaire de l’eau (N) ;
• dS = la surface élémentaire d’application de la force sur la paroi (m2).
• τ = la contrainte tractrice (N.m–2) ;
• dFt = la force de frottement élémentaire de l’eau (N) ;
• dS = la surface élémentaire d’application de la force sur la paroi (m2).
En écoulement uniforme, la contrainte tractrice au fond du lit peut être calculée à partir de la formule suivante :

Où :
• τ = la contrainte tractrice (N.m–2) ;
• ρ = la masse volumique de l’eau (kg.m–3) ;
• g = l’accélération de pesanteur (m.s–2) ;
• R = le rayon hydraulique (m) ;
• j = la perte de charge linéaire (adimensionnel).
• τ = la contrainte tractrice (N.m–2) ;
• ρ = la masse volumique de l’eau (kg.m–3) ;
• g = l’accélération de pesanteur (m.s–2) ;
• R = le rayon hydraulique (m) ;
• j = la perte de charge linéaire (adimensionnel).
Des hypothèses de calcul permettent de simplifier cette expression : la ligne d’énergie (j) est parfois remplacée par la pente (i) du cours d’eau pour simplifier les calculs (équivaut à se placer dans le cas d’un écoulement uniforme). Sur les cours d’eau suffisamment larges (L > 20 R), on peut remplacer le rayon hydraulique (R) par la hauteur d’eau (h).
Sur une berge immergée, la force de pesanteur s’ajoute à la force tractrice pour la mise en mouvement des matériaux. Ainsi, plus la berge est inclinée, plus il est facile de mettre les particules en mouvement.
Lorsque cette contrainte atteint un seuil critique, elle est responsable de la mise en mouvement des matériaux du fond du lit ou de la berge. Nous parlons alors de « contrainte tractrice critique ».
L’expression de la contrainte tractrice critique sur les berges fait intervenir l’angle de frottement interne φ du matériau constituant le sol et la pente de la berge β :

Où :
• τβ = la contrainte tractrice critique sur une pente d’angle β avec l’horizontale (N.m–2) ;
• φ = l’angle de frottement interne du sol (°) ;
• τ = la contrainte tractrice moyenne exercée par le fluide sur la paroi (N.m–2).
• τβ = la contrainte tractrice critique sur une pente d’angle β avec l’horizontale (N.m–2) ;
• φ = l’angle de frottement interne du sol (°) ;
• τ = la contrainte tractrice moyenne exercée par le fluide sur la paroi (N.m–2).
Il est d’usage d’évaluer la contrainte tractrice moyenne sur les berges équivalente à 0,75 fois la contrainte maximale sur le fond du lit, mais la validité de cette approximation reste à démontrer pour les rivières de montagne.
La poussée stabilisatrice du cours d’eau sur la berge

Où :
• dP = la pression de l’eau (N.m–2) sur la surface dS (m2) ;
• ρ = la masse volumique de l’eau (kg.m–3) ;
• g = l’accélération de pesanteur (m.s–2) ;
• h = la hauteur de la colonne d’eau (m).
• dP = la pression de l’eau (N.m–2) sur la surface dS (m2) ;
• ρ = la masse volumique de l’eau (kg.m–3) ;
• g = l’accélération de pesanteur (m.s–2) ;
• h = la hauteur de la colonne d’eau (m).
La profondeur d’affouillement
Il existe deux types d’enfoncement du fond du lit : les incisions généralisées qui s’étendent sur un tronçon de cours d’eau et les affouillements localisés liés à une singularité hydraulique (rétrécissement, embâcle, etc.).
La formule d’Izard et Bradley retravaillée par Ramette permet de calculer la profondeur d’affouillement ou la profondeur sur laquelle les matériaux du lit risquent d’être déplacés (Ramette 1981). Cette formule n’est valable que pour un affouillement localisé au droit d’un rétrécissement, elle n’est pas applicable pour un tronçon homogène :
E = Y – h

Où :
• E = l’épaisseur d’affouillement (m) ;
• Y = la profondeur du fond du lit en mouvement sous eau (m) ;
• h = le tirant d’eau (m) ;
• Q = le débit liquide (m3.sm–1) ;
• L = la largeur du cours d’eau (m) ;
• D = le diamètre des matériaux du fond du lit (m).
À noter que cette formule n’est qu’indicative, et que la profondeur de mise en mouvement des matériaux lors des crues est peu connue, notamment sur les cours d’eau à forte pente.